The Harmonies of Nature

Version française...

Béla Bartók is seen in our day as one of the twentieth century’s major composers, but we all too often forget that he first became known as a pianist and ethnomusicologist. Accompanied by his friend and colleague, Zoltan Kodály, he travelled the byways of Eastern Europe from 1907 to 1918, gathering thousands of folk songs, work that was to have a decisive influence on Bartók as a composer. In particular, he wove into his own works the modal forms and irregular rhythms typical of many of the folk songs gathered at this time.
In the opening bars of Music for Strings, Percussion, and Celesta (1937), for example, Bartók uses metrical changes to mark the successive entries in the fugue and the ever increasing, arching melodic cadences that remind the listener of certain Eastern European laments. The tightly woven nature of these initial melodies comes from the small intervals found in an artificial scale based on a mode often used in gypsy music (Ex. 1a). The main feature of this mode as employed by Bartók is the alternation between the minor third interval and the pair of minor seconds. He gets new pitches by changing the order of intervals in the descending version of the scale (Ex. 1b). This addition of seemingly “foreign” notes to a very oriental-sounding scale is one of Bartók’s key techniques for deftly combining folk and modern elements in his music.

1. The tonal axes system
In Bartók’s work, nevertheless, modernism is always firmly rooted in a tonal hierarchy. Ernö Lendvai has provided an ingenious explanation of Bartók’s approach according to what he calls “the tonal axes system.” Lendvai starts with the principle that all notes that fall within the circle of fifths (or fourths, depending on the direction you are moving) have one of three functions: tonic (T), dominant (D), or subdominant (S).
For example, if we establish C as the tonic, its lower neighbour in the circle (F) will be its subdominant, and its upper neighbour (G) its dominant. If we move upwards through the circle we come to D, A, and E. These notes are also the relative minors of F, C, and G major, and naturally assume the same functions. Thus the notes D, A, and E belong respectively to the subdominant, tonic, and dominant axes. It is then obvious that the sequence T-D-S is repeated. From this, Lendvai deduces that after following the circle of fifths through every note of the chromatic scale, the six remaining notes will also assume the alternating functions of tonic, dominant, and subdominant (Ex. 2). As a result, the tonic axis is made up of the notes C-A-F#-Eb, the dominant axis of the notes G-E-C#-Bb, and the subdominant axis of the notes F-D-B-Ab.
In analyzing Music for Strings, Percussion, and Celesta, we can see that Bartók did indeed follow a tonal plan of this nature, and that each movement is based on one of the notes of the tonic axis:

MOVEMENT BEGINNING MIDDLE END
I A Eb (bar 56) A
> II C F# (bar 263) C
> III F# C (bar 46) F#
IV A Eb (bar 83) A
> (Lendvai, p. 4)

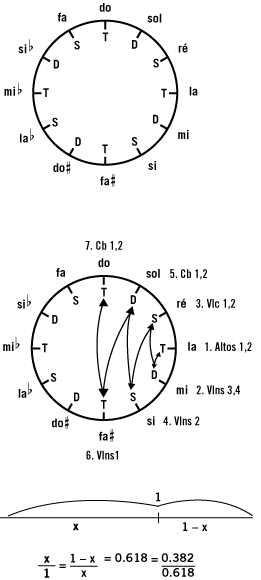
Bartók’s preoccupation with tonal axes can be seen in the progress of each movement. It is sufficient, for example, to take the first notes of the successive fugue entries in the first movement to establish the tonal progression or trajectory A-E-D-B-G-F#-C. This trajectory can be harmoniously transposed on the tonal axes chart (Ex. 3).

The two last entries by the first violins on F# (bar 25) and by the cellos and double basses on C (bar 27) bring the fugue’s initial statement to an end, heralding the transition to the entry of the kettledrum at bar 34. It is worth noting that the composer has chosen the two poles of the tonic axis to emphasize the importance of this formal moment.

2. The Golden Ratio and the Fibonacci sequence

For Bartók, the choice of pitches is not the main criterion in planning the form of a composition. “We follow the nature of the composition,” he liked to say. Bartók was fascinated by regular structures found in nature, such as the spirals of a snail shell or the perfectly ordered rows of a pine cone — both examples of a rule of natural architecture generally called “the Golden Ratio” or the “Golden Mean.” In geometrical terms, this rule states that a unit can be divided in two in such a way that the ratio of the greater part to the whole is the same as the ratio of the smaller part to the greater part (Ex. 4).

In numerical terms, an irrational number of the order of 0.618 for the greater section is obtained, and of 0.382 for the smaller section. Note the fact that these proportions are exactly those observed in the concentric circles of a snail shell or pine cone. Bartók made continual use of these proportions to determine the relative duration of different sections in his works.

The use of an irrational number presents certain difficulties, nevertheless. A simple mathematical series enables us to get around the problem and approach The Golden Ratio with a small margin of error. This series is called “the Fibonacci sequence.” The sequence is calculated by adding to a number its immediate predecessor in the series: 0 + 1 = 1, 1 + 1 = 2, 2 + 1 = 3, 3 + 2 = 5, etc., which gives 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 and so on. As one advances in the sequence, one gets closer to The Golden Ratio by dividing any given number by its successor.

The first movement of Music for Strings, Percussion, and Celesta is one of the finest examples of formal construction along these lines. If we take another look at the movement’s opening bars, we find that the fugue entries correspond to the numbers of the following bars:

Violas 1, 2 : bar 1
Violas 3, 4 : bar 5
Cellos 1, 2 : bar 8
Violins 2 : bar 13
Double bass : bar 18
Violins 1 : bar 27

The first four entries correspond to the Fibonacci Sequence. Missing are the numbers 2, 3, and 21. In bars 2 and 3, the violas state the second and third phrases of the theme, clearly defined by a half-rest. Bar 21 marks the end of the statement of the theme by the doubles basses and initiates a short passage before the first violins enter at bar 27. As mentioned earlier, this is where the transition begins, leading to the kettledrum entry at bar 34, another number in the Fibonacci sequence.

How are we to explain the entries in bars 18 and 27, in this case? Here we must consider purely practical reasons for Bartók’s choice. It is a given that the further one advances in the Fibonacci sequence, the greater the amount of time needed by the music to reach the desired bar so as to establish an important formal moment. Bartók has to find a way to insert his less significant musical moments between the major formal frontiers. He solves the problem by making subdivisions within the major sections defined by the sequence. Thus, from bar 13 (entry of the second violins) to bar 21 (beginning of passage), there are 8 bars. Divide this into two subgroups of 5 and 3 bars respectively (5:3 is a Fibonacci ratio), and we get the double bass entry at bar 18. Similarly, there are 21 bars in the passage from bar 13 to bar 34; if we subdivide these into groups of 14 and 7 bars respectively (a Fibonacci ratio of 2:1) we get the entry of violins at bar 27.

Conclusion : an art that unites beauty and balance
We would need far more space than is available here to do justice to Bartók’s undeniable genius. Take the structures of sound, for example. Do they, too, correspond to the composer’s preoccupation with nature’s architecture? Seen from this perspective, the melodic and harmonic intervals in Music for Strings, Percussion, and Celesta are indeed chosen on the basis of the Fibonacci sequence — but that’s a subject for another article.
The few examples illustrated here are given only to show how concerned Bartók was about conceiving each work as a harmonious whole governed by a single, universal law. This concern for balance made him very much a composer of his time in an era in which science was desperately striving to explain the universe by a “unique, simple, and beautiful” principle, as Einstein put it. The scientists have yet to do this, but Bartók, through his music, has at least given us the vivid illusion of such unique and simple beauty. n
[Translated by Jane Brierley]